1. 문제 링크
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
2. 문제 및 입출력예제
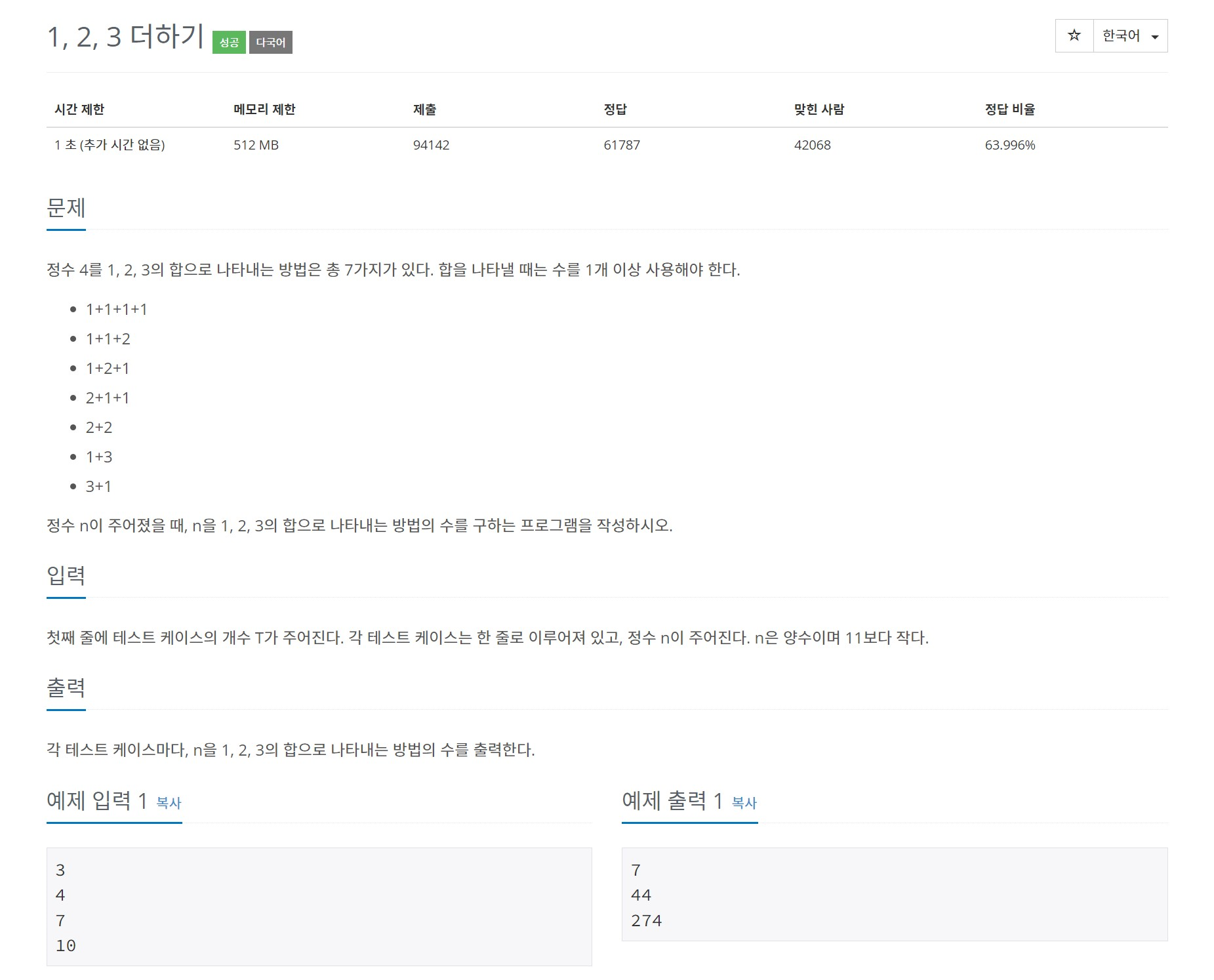
3. 문제 풀이
n은 최대 10이다.
근데 4를 만들때 쓴 녀석들에 1씩을 더하면 5를 만들 수 있다.
그니까 각자 만든거에 1을 더한 경우들을 더하고 각 숫자만 넣으면 되는것 같다.
1은 1 (1개)
2는 11 2 (2개)
3은 111 21 12 3 (4개)
4는 1/111 1/21 1/12 1/3 111/1(중복) 21/1 12/1(중복) 3/1 11/2(중복) 2/11(1과 3의 경우, 2끼리 경우의 합)
=> 4는 1111 112 121 211 22 13 31 (7개) 1 2 4
5는 1과 4, 2와 3
1 다음 4 (7개)
1/1111 1/112 1/121 1/211 1/22 1/13 1/31
4 다음 1 (3개)
1111/1(중복) 112/1(중복) 121/1(중복) 211/1 22/1 13/1(중복) 31/1
2 다음 3 (2개)
11/111(중복) 11/21(중복) 11/12(중복) 11/3(중복) 2/111(중복) 2/21(중복) 2/12 2/3
3 다음 2 (1개)
111/11(중복) 21/11(중복) 12/11(중복) 3/11(중복) 111/2(중복) 21/2(중복) 12/2(중복) 3/2
총 13개 2 4 7
6는 2와 4의 경우, 3끼리 경우 합 인가?
2 다음 4 (14개)
11/1111 11/112 11/121 11/211 11/22 11/13 11/31
2/1111 2/112 2/121 2/211 2/22 2/13 2/31
111111 11112 11121 11211 1122 1113 1131 21111 2112 2121 2211 222 213 231
4 다음 2 (6개)
1111/11(중복) 112/11(중복) 121/11 211/11(중복) 22/11(중복) 13/11 31/11
1111/2(중복) 112/2(중복) 121/2 211/2(중복) 22/2(중복) 13/2 31/2
12111 1311 3111 1212 132 312
3끼리 (4개)
111/111(중복) 111/21(중복) 111/12(중복) 111/3(중복)
21/111(중복) 21/21(중복) 21/12(중복) 21/3(중복)
12/111(중복) 12/21 12/12(중복) 12/3
3/111(중복) 3/21 3/12(중복) 3/3
1221 123 321 33
총 24개 4 7 13
4. 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
for(int t=0;t<T;t++) {
int n = Integer.parseInt(br.readLine());
int[] sum = new int[10];
sum[0] = 1;
sum[1] = 2;
sum[2] = 4;
for(int i=3;i<10;i++) {
sum[i] = sum[i-1]+ sum[i-2] + sum[i-3];
}
sb.append(sum[n-1]+"\n");
}
System.out.println(sb);
}
}
'ALGORITHM' 카테고리의 다른 글
| 백준 15650 N과 M (2) (Java) (0) | 2023.02.10 |
|---|---|
| 백준 15649 N과 M (Java) (0) | 2023.02.09 |
| 백준 17478 재귀함수가 뭔가요? (Java) (0) | 2023.02.07 |
| 백준 1476 날짜 계산 (Java) (0) | 2023.02.06 |
| 백준 3085 사탕 게임 (Java) (0) | 2023.02.05 |



